2023年成考专升本每日一练《高等数学二》10月5日专为备考2023年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设事件A、B互不相容,P(A)=0.3,P(B)=0.2,则P(A+B)=().
- A:0.44
- B:0.5
- C:0.1
- D:0.06
答 案:B
解 析:事件A、B互不相容,则P(AB)=0,故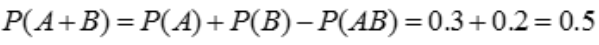 .
.
2、设f(x)为连续函数,则 =()
=()
- A:f(2)-f(0)
- B:2[f(2)-f(0)]
- C:

- D:

答 案:C
解 析: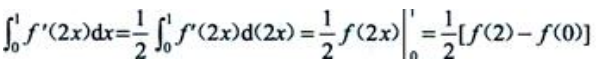
主观题
1、设函数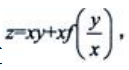 其中是f(u)二阶可微的.
其中是f(u)二阶可微的.
答 案:证明: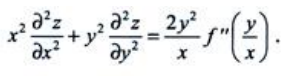 证:分别将z对x和y求偏导得
证:分别将z对x和y求偏导得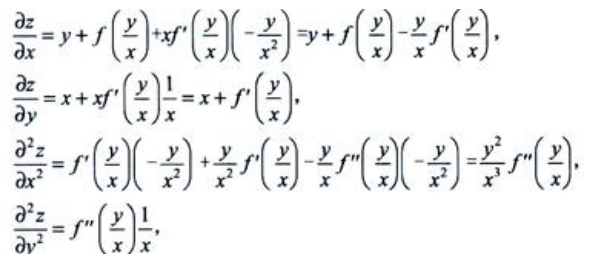 所以
所以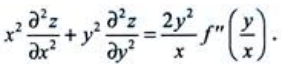
2、一枚2分硬币,连续抛掷3次,设A={至少有一次国徽向上}.求P(A).
答 案:解:一枚2分硬币连续抛掷3次出现的基本事件共有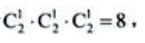 则
则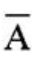 ={全部是字面向上},
={全部是字面向上},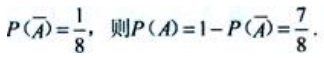
填空题
1、斜边长为l的直角三角形中,最大周长为()
答 案:(1+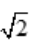 )l
)l
解 析:该题也是条件极值问题,用拉格朗日乘数法求解,设直角三角形的两直角边长分别为x和y,周长为z,且z=l+x+y(0<x<l,0<y<l),条件函数为l2=x2+y2.令F(x,y,λ)=l+x+y+λ(x2+y2-l2)求解方程组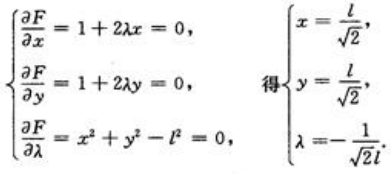 根据实际意义,一定存在最大周长,所x=y=
根据实际意义,一定存在最大周长,所x=y=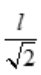 时,即斜边长为l时的等腰直角三角形周长最大,且此周长为(1+
时,即斜边长为l时的等腰直角三角形周长最大,且此周长为(1+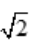 )l.
)l.
2、函数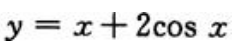 在
在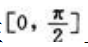 上最大值为().
上最大值为().
答 案: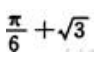
解 析:由 得驻点为
得驻点为 ,
, ,比较得y的最大值为
,比较得y的最大值为
简答题
1、计算
答 案:由洛必达法则有
2、计算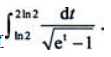
答 案: 设
设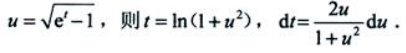 则
则
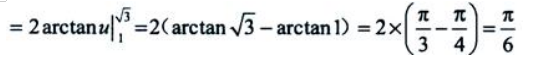
精彩评论